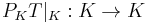Compression (functional analysis)

In functional analysis, the compression of a linear operator T on a Hilbert space to a subspace K is the operator

$P_K T \vert_K�: K \rightarrow K$

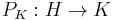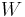where $P_K�: H \rightarrow K$ is the orthogonal projection onto K. This is a natural way to obtain an operator on K from an operator on the whole Hilbert space. If K is an invariant subspace for T, then the compression of T to K is the restricted operator K→K sending k to Tk. General, let $V$ be isometry on Hilbert space $W$ , subspace of Hilbert space $H$ (T on $H$ ). 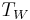We define compression $T_W$ of a linear operator T on a Hilbert space $H$ to a subspace W as linear operator $V^*TV$ . 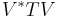If T is hermitian operator, then compression is hermitian too. When replace V with identity 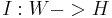$I: W -> H$ (that implies 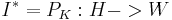$I^*=P_K�: H -> W$ ), we encounter special definition.

References

P. Halmos, A Hilbert Space Problem Book, Second Edition, Springer-Verlag, 1982.

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›

Compression (functional analysis)

See also

References